El profesor que enseña matemáticas con caramelos, piezas de Lego y una olla
A través del fútbol y del baloncesto los niños pueden aprender conceptos geométricos y de cálculos matemáticos
- Caramelos, piezas de Lego o una olla para enseñar matemáticas a los niños
¿Quién ha dicho que las matemáticas son aburridas? Eso es porque no conocen el innovador método de un profesor andaluz que enseña matemáticas y conceptos tan 'complejos' como el número Pi o el teorema de Pitágoras con caramelos, piezas de Lego o con una tapa de una olla y una cuerda. ¿Quieres conocer su historia? Después de leer, ¡solo querrás volver a las aulas!
Caramelos, piezas de Lego o una olla para enseñar matemáticas a los niños

Las matemáticas son muy importantes en la vida de cualquier persona porque se presentan en todas la facetas de nuestra vida a todos los niveles. Las usamos todos, desde el abuelo que va a comprar el periódico y mira su viejo reloj para saber la hora, pasando por un millennial que busca un vuelo barato de última hora por internet, hasta el científico más experimentado en astrofísica u otras materias.
Quizás, por esto, Sergio Guirado, un profesor andaluz de matemáticas, ha querido darle a esta asignatura la importancia que merecen. Sergio ha creado su particular método para enseñar matemáticas a los chavales de primero, segundo, tercero y cuarto de la E.S.O.
- Lo que pretendo es que los alumnos memoricen lo menos posible y que intenten deducir por sí solos. Y para conseguir esto, lo más importante es darles un por qué y un para qué, enseñándoles el origen de las cosas. Y es que, yo soy de los que cree que las matemáticas se puedan tocar, explica el profesor.
Trabajar con elementos cercanos al mundo de los niños y objetos de su interés es la base de este innovador método de este profesor de matemáticas. Y así como en la mesa de sus clases te puedes encontrar caramelos, un tapa de una olla o hasta piezas de Lego.
1. Teorema de Pitágoras con caramelos
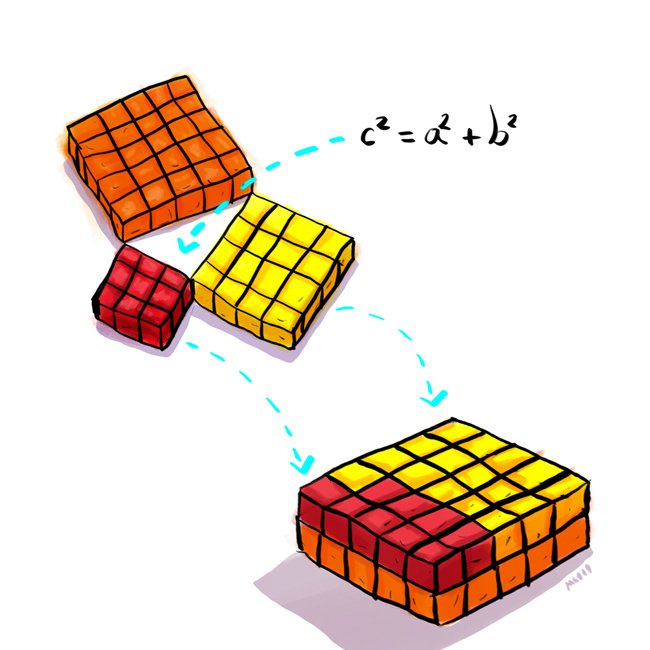
- Lo que explico con los caramelos sugus (son cuadrados) es la demostración geométrica del teorema. Es algo como esto: El triángulo blanco que se ve entre los tres cuadrados es un triángulo rectángulo y todo triángulo rectángulo verifica que c²=a² +b² (Siempre que hablamos de c²=, hablamos del área de un cuadrado de lado c)", dice y añade: "En este caso, el área del cuadrado formado por sugus naranja 5², es igual a la suma del área del cuadrado de sugus rojos 3² más el área del cuadrado formado por sugus amarillos 4². Para demostrarlo, superponemos los 9 sugus rojos y los 16 amarillos sobre los 25 naranja hasta cubrir la totalidad de la superficie naranja, explica Guirado.
2. Factores primos con piezas de Lego
Con las piezas de Lego, Sergio explica la descomposición en factores primos y la divisibilidad.
- Si varias piezas de Lego están juntas, se interpretan como multiplicación de números primos. Las iremos separando hasta descomponer en piezas simples que representarán la factorización, explica.
3. Figuras geométricas a través del fútbol y el baloncesto
- Tanto en el fútbol como en el baloncesto existen muchos conceptos geométricos: polígonos, como el rectángulo de juego; circunferencias, como la del centro del campo; diagonales y triangulaciones que realizan los jugadores; esferas representadas con el balón, etc. Por eso no es difícil relacionar las áreas y su cálculo con estos dos deportes, señala Guirado.
4. El número pi explicado con una olla
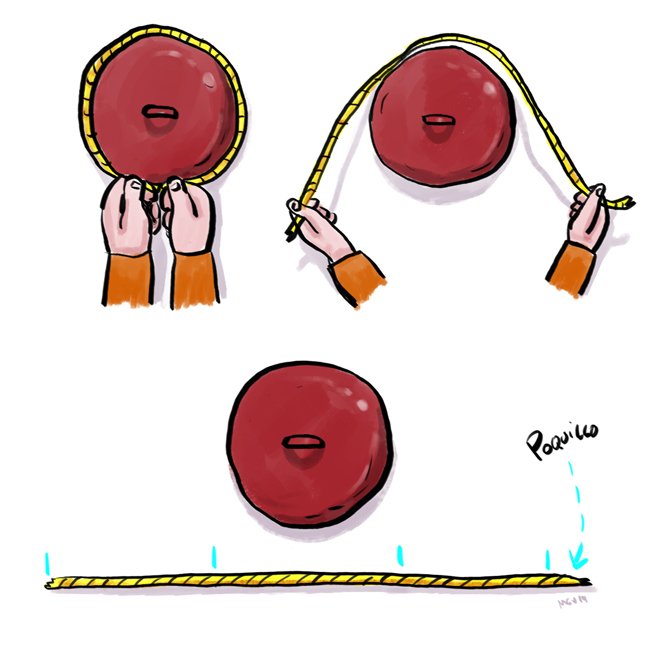
- El perímetro de una circunferencia es tres veces y un poquillo la medida del diámetro de esta. Ese tres veces y un poquillo es lo que en matemáticas se denomina Pi. Para demostrarlo, cogemos la tapa de una olla y la rodeamos con una cuerda, luego abrimos la cuerda y comprobamos que la medida de esta es tres veces y un poco la medida del diámetro de la tapa, afirma el profesor.
Y, todo esto lo hace Sergio para evitar siempre la abstracción. ¿Cómo?
- Cuando estudiamos las fracciones, hacemos un trabajo de investigación utilizando páginas de búsqueda de hoteles. Si en el pueblo hay un determinado número de alojamientos, vemos qué proporción de ellos son hoteles, bed and breakfast, casas rurales, etc....
Al final de sus clases, los chavales, además de aprender matemáticas, se lo han pasado bien y Sergio está feliz y satisfecho. Cuando comenzó a enseñar matemáticas con objetos cotidianos él solo buscaba evitar las caras de aburrimiento de los alumnos. ¡Objetivo conseguido!
Puedes leer más artículos similares a El profesor que enseña matemáticas con caramelos, piezas de Lego y una olla, en la categoría de Matemáticas en Guiainfantil.com.
Publicado:
Actualizado: